维也纳科技大学青年学者Juan P. Aguilera博士“可靠性谱系”线上讲座顺利举行
点击次数: 更新时间:2023-06-15
本网讯(通讯员 杨新宇)6月7日晚,维也纳科技大学青年学者Juan P. Aguilera博士通过学术志平台作了题为“可靠性谱系(聚焦于 ![]() )”(Soundness Spectrum(with particular focus on
)”(Soundness Spectrum(with particular focus on ![]() ))的线上讲座。本次讲座由太阳程勇教授主持,海内外380余名听众参与本次讲座。
))的线上讲座。本次讲座由太阳程勇教授主持,海内外380余名听众参与本次讲座。
首先程勇教授向听众介绍了主讲人,Aguilera博士是优秀青年学者,他目前担任多个大学的研究职位,他的研究领域涉及数理逻辑的许多分支,他的博士论文获得了来自国际逻辑、语言与信息协会、奥地利数学协会和德国数理逻辑协会的多个奖项。
传统序数分析依赖于序数表示系统,在研究具有更高复杂性理论的证明论强度时遇到瓶颈。Aguilera博士的讲座提出了一种研究序数分析的更抽象的框架,在其中用比序数更抽象的对象替代序数。这种框架提供了一种将传统序数分析扩展到具有更高复杂度的对象的一般方法。
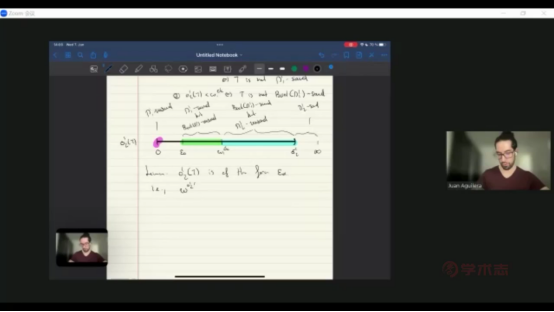
Aguilera博士的讲座从序数分析的经典结论开始。 对于一个递归可枚举理论T且T是ACA0的扩张,经典序数分析关注可证递归良序的上确界—— ![]() ,如
,如 ![]() 。
。 ![]() 可以看作是对理论T的
可以看作是对理论T的 ![]() 真后承的刻画。一个自然的问题是:能否定义
真后承的刻画。一个自然的问题是:能否定义 ![]() 来刻画理论T的
来刻画理论T的 ![]() 后承。然而困难是序数并不能完成这一任务,我们需要使用更抽象的对象——dilator。
后承。然而困难是序数并不能完成这一任务,我们需要使用更抽象的对象——dilator。
Aguilera博士对dilator的定义使用了范畴论语言,dilator是满足一定条件(对正向极限(direct limit)和拉回(pullback)交换)的序数范畴上的函子。我们可以用实数编码一个dilator。因此 ![]() 可以定义为:最小的dilatorD使得对于任意dilatorF,若T⊢ “Fis adilator”,则F可以嵌入到D中。进而我们可以证明对于
可以定义为:最小的dilatorD使得对于任意dilatorF,若T⊢ “Fis adilator”,则F可以嵌入到D中。进而我们可以证明对于 ![]() -可靠的理论T,
-可靠的理论T, ![]() 存在并且是递归的。而对于
存在并且是递归的。而对于 ![]() -不可靠的理论T,我们虽然无法定义
-不可靠的理论T,我们虽然无法定义 ![]() ,但却可以用序数去刻画。此时存在拟dilatorD使得T⊢ “D is a dilator”但实际上D不是dilator,这就意味着存在序数α 使得D(α)不是序数,最小的满足这一性质的序数记为
,但却可以用序数去刻画。此时存在拟dilatorD使得T⊢ “D is a dilator”但实际上D不是dilator,这就意味着存在序数α 使得D(α)不是序数,最小的满足这一性质的序数记为 ![]() 。
。
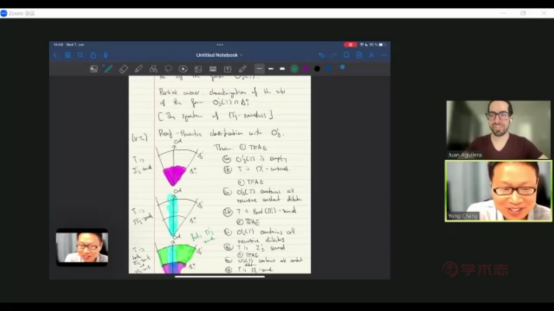
讲座的重心是对 ![]() 的证明论分类。Aguilera博士给出了如下的可靠性谱系:(A)
的证明论分类。Aguilera博士给出了如下的可靠性谱系:(A) ![]() 当且仅当
当且仅当 ![]() 当且仅当T是
当且仅当T是 ![]() -不可靠的;(B)
-不可靠的;(B) ![]() 是非零递归的当且仅当
是非零递归的当且仅当 ![]() ≤
≤ ![]() 当且仅当T是
当且仅当T是 ![]() -可靠但是Boole(
-可靠但是Boole( ![]() -不可靠的;(C)
-不可靠的;(C) ![]() 是非递归的当且仅当
是非递归的当且仅当 ![]() ≤
≤ ![]() 当且仅当T是Boole(
当且仅当T是Boole( ![]() -可靠但是
-可靠但是 ![]() -不可靠的;(D)
-不可靠的;(D) ![]() ≤
≤ ![]() 当且仅当T是
当且仅当T是 ![]() -可靠的。
-可靠的。
进而Aguilera博士证明了 ![]() 形如
形如 ![]() (即
(即 ![]() )并且是
)并且是 ![]() -可定义的。一个开问题是对于任何满足以上两个性质的序数α, 是否存在一个
-可定义的。一个开问题是对于任何满足以上两个性质的序数α, 是否存在一个 ![]() 的递归可枚举扩张T使得
的递归可枚举扩张T使得 ![]() 恰好为α,该问题被称为“
恰好为α,该问题被称为“ ![]() 谱系猜想”。在ATR0中可以证明,若
谱系猜想”。在ATR0中可以证明,若 ![]() 谱系猜想不成立,则二阶算术是一致的。因此
谱系猜想不成立,则二阶算术是一致的。因此 ![]() 谱系猜想与二阶算术相容。
谱系猜想与二阶算术相容。
最后,Aguilera博士讨论了 ![]() 以及
以及 ![]() 的情形。此时我们需要比dilator更抽象的对象——ptyx。一个0-ptyx是一个序数,而(n+1)-ptyx是从n-ptyx范畴到良序范畴的满足对正向极限和拉回交换的函子。基于ptyx的概念,我们可以类似地定义
的情形。此时我们需要比dilator更抽象的对象——ptyx。一个0-ptyx是一个序数,而(n+1)-ptyx是从n-ptyx范畴到良序范畴的满足对正向极限和拉回交换的函子。基于ptyx的概念,我们可以类似地定义 ![]() 。类似于
。类似于 ![]() 的情形,我们可以定义
的情形,我们可以定义 ![]() 并且得到
并且得到 ![]() 的可靠性谱系。
的可靠性谱系。
在提问环节,山东大学哲学与社会发展学院梁飞副教授提出了两个问题:1.这种分类从证明论的视角有什么具体的意义?2.本次讲座的主题能否与结构证明论建立联系?
对于第一个问题,Aguilera博士指出 ![]() 和
和 ![]() 的情形和熟知的
的情形和熟知的 ![]() 情形有很大的不同,证明论学家通常关注的是可靠的理论,但在
情形有很大的不同,证明论学家通常关注的是可靠的理论,但在 ![]() 和
和 ![]() 的情形中不可靠的理论扮演了关键的角色,这是非常有趣的,为我们展现了深刻而优美的图景。另外,
的情形中不可靠的理论扮演了关键的角色,这是非常有趣的,为我们展现了深刻而优美的图景。另外, ![]() 和
和 ![]() 不可靠的理论与ZFC的扩张有着密切的联系,可以期待未来在这方面的应用。对于第二个问题,Aguilera博士指出这次讲座的主题主要基于无穷证明论的传统,而结构证明论关注的是有穷的证明结构,比如cut-free证明的复杂性,但无穷证明论关注的是能否可证而并非实际证明如何。
不可靠的理论与ZFC的扩张有着密切的联系,可以期待未来在这方面的应用。对于第二个问题,Aguilera博士指出这次讲座的主题主要基于无穷证明论的传统,而结构证明论关注的是有穷的证明结构,比如cut-free证明的复杂性,但无穷证明论关注的是能否可证而并非实际证明如何。
程勇教授也提出了三个问题:1. Aguilera博士是否认为 ![]() 谱系猜想成立?2. 本次讲座中使用的dilator和通常的序数表示系统的联系;3. Aguilera博士是否考虑过将这一技术应用于Rathjen教授提出的关于确定
谱系猜想成立?2. 本次讲座中使用的dilator和通常的序数表示系统的联系;3. Aguilera博士是否考虑过将这一技术应用于Rathjen教授提出的关于确定 ![]() -comprehension理论的证明论序数的开问题。对于第一个问题,Aguilera博士认为有证据表明
-comprehension理论的证明论序数的开问题。对于第一个问题,Aguilera博士认为有证据表明 ![]() 谱系猜想不成立,但不排除其成立的可能;对于第二个问题,Aguilera博士指出在同构意义上dilator可以看作一种序数表示系统;对于第三个问题,Aguilera博士表示尚未考虑过这一应用。
谱系猜想不成立,但不排除其成立的可能;对于第二个问题,Aguilera博士指出在同构意义上dilator可以看作一种序数表示系统;对于第三个问题,Aguilera博士表示尚未考虑过这一应用。
最后,程勇教授感谢Aguilera博士带来的精彩讲座。至此,本次讲座圆满结束。
(编辑:邓莉萍 审稿:严璨)
